Normalerweise starten Unternehmen damit zunächst eine große Anzahl neuer Nutzer anzuziehen und zu einem späteren Zeitpunkt Gewinn zu erwirtschaften. Ab einem bestimmten Punkt konzentrieren Unternehmen ihre Strategien darauf, bestehende Kunden an sich zu binden, da Kunden zu halten deutlich kostengünstiger ist als neue Kunden zu gewinnen. Das ist der Moment, an dem „Customer Churn“ eine wichtige Rolle spielt. Es ist eine Statistik, die beschreibt wieviele Kunden ein Unternehmen verlassen. Churn Modeling ist eine Methode, um zu verstehen, warum Kunden wechseln und das zu verhindern. In diesem Beitrag zeigen wir, wie man Churn in Python berechnen kann.
Customer Churn verstehen
Was bedeutet Customer Churn?
Customer Churn bedeutet, dass ein Kunde die Bindung zu einem Unternehmen beendet.
Warum wechseln Kunden?
Obwohl es einige Faktoren gibt, die den Wechsel beeinflussen, läuft es meist dennoch auf einen der folgenden Gründe hinaus:
- Der Kunde ist frustriert von der Produkterfahrung
- Die Kosten für das Produkt übersteigen dessen Wert
- Dem Produkt fehlt ein angebrachter Kundensupport
- Die falschen Kunden werden angezogen
Warum es wichtig ist Churn zu verstehen
Neue Kunden zu gewinnen, kann oftmals deutlich teurer sein, als an bereits bestehende Kunden zu verkaufen. Zu verstehen, was den Wechsel verursacht und warum Kunden abwandern ist wichtig, um Kunden zur erneuten Nutzung des Produktes zu bewegen. In der Lage zu sein, Kunden mit einer hohen Wechselwahrscheinlichkeit zu finden, kann uns helfen, passende Marketingstrategien zu gestalten und Kunden zu binden.
Daten
Die notwendigen Daten können in der folgenden GitHub Bibliothek heruntergeladen werden.
Wir arbeiten mit den Kundendaten eines Telefonanbieters. Die Daten haben 7043 Einträge und 20 Variablen, die die binäre Zielvariable Churn beinhalten.
Vorgehensweise
- 1) EDA-Mit welchen Daten arbeiten wir?
- 2) Mit welchen Daten arbeiten wir?
- 3) Trainingszeit-Modelle bauen und vergleichen
- 4) Vorhersagen und Modellbeurteilung
- 5) Fazit und abschließende Gedanken
Hands-On!
Genug geredet, lasst uns direkt die Bibliotheken importieren, die wir brauchen…
## Basics
import numpy as np
import pandas as pd
## Visualization
import matplotlib as plt
import matplotlib.pyplot as plt
import seaborn as sns
## ML
from sklearn.model_selection import train_test_split,
cross_val_score, GridSearchCV
from sklearn.preprocessing import OneHotEncoder, StandardScaler
from sklearn.impute import SimpleImputer
from sklearn.pipeline import Pipeline
from sklearn.feature_selection import SelectKBest
from sklearn.compose import ColumnTransformer
from sklearn.metrics import accuracy_score,
classification_report, roc_auc_score, plot_roc_curve
## Algorithms
from sklearn.neighbors import KNeighborsClassifier
from sklearn.svm import SVC
from sklearn.tree import DecisionTreeClassifier
from sklearn.ensemble import RandomForestClassifier,
AdaBoostClassifier, GradientBoostingClassifier
… und die Daten:
data_raw = pd.read_csv('https://raw.githubusercontent.com/lucamarcelo/Churn-Modeling/main/Customer%20Churn%20Data.csv', set_index='CustomerID')
## Split the data to create a train and test set
train, test = train_test_split(data_raw, test_size=0.25)
1. Explorative Datenanalyse- Mit welchen Daten arbeiten wir?
Zu verstehen, mit welchen Daten wir arbeiten, erlaubt es uns bessere Entscheidungen zu treffen, wenn es darum geht, welche Vorverarbeitungen wir anwenden müssen, welchen Klassifikator wir wählen und wie wir die Ergebnisse interpretieren.
Datentypen betrachten und falsch codierte Daten korrigieren
data_raw.dtypes
## We have one variable that's wrongly encoded as string
data_raw['TotalCharges'] =pd.to_numeric(data_raw['TotalCharges'], errors='coerce')
Fehlende Werte und Kardinalität
Der Begriff Kardinalität bezieht sich auf die Anzahl einzigartiger Werte der kategorischen Variablen. Die folgende Funktion erlaubt es uns, fehlende Werte und Kardinalität zu finden.
def missing_values(data):
df = pd.DataFrame()
for col in list(data):
unique_values = data[col].unique()
try:
unique_values = np.sort(unique_values)
except:
pass
nans = round(pd.isna(data[col]).sum()/data.shape[0]*100, 1)
zeros = round((data[col] == 0).sum()/data.shape[0]*100, 1)
#empty = round((data[data[col]] '').sum()/data.shape[0]*100,1)
df = df.append(pd.DataFrame([col, len(unique_values), nans, zeros]).T, ignore_index = True)
return df.rename(columns = {0: 'variable',
1: 'Unique values',
2: 'Nan %',
3: 'zeros %',
#4: 'empty'}).sort_values('Nan %', ascending=False)
missing_values(data_raw)
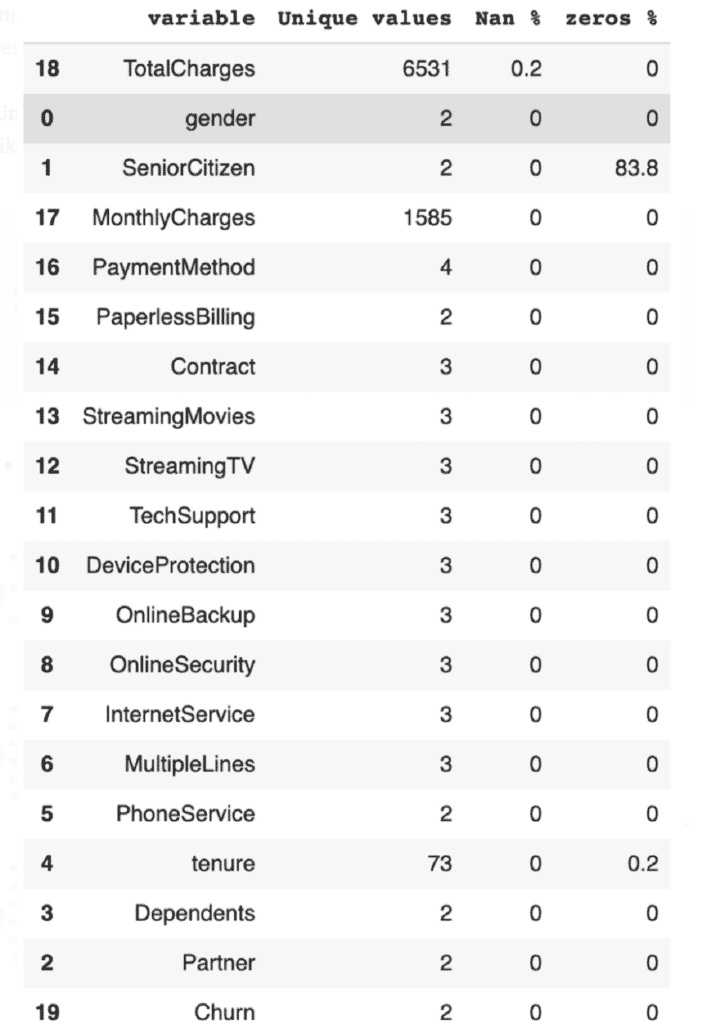
- Ergebnis:
Wie man sehen kann, gibt es nurNaNsinTotalCharges,um die wir uns in der Vorverarbeitung kümmern. Alle kategorischen Variablen haben eine relativ geringe Kardinalität. Das ist wichtig, wenn es um die Wahl der Codierung geht.
Verteilung
In der univariaten Analyse, betrachten wir eine einzige Variable, während wir in der bivariaten und multivariaten Analyse zwei oder mehr Variablen betrachten.
Bei der Univariaten Analyse erhalten wir für jede unserer Variablen ein Histogramm. Am besten löst man das, indem man eine Grafik mit allen Histogrammen erstellt.
fig, ax = plt.subplots(4, 5, figsize=(15, 12))
plt.subplots_adjust(left=None, bottom=None, right=None, top=1, wspace=0.3, hspace=0.4)
for variable, subplot in zip(data_raw.columns, ax.flatten()):
sns.histplot(data_raw[variable], ax=subplot)
- Ergebnis:
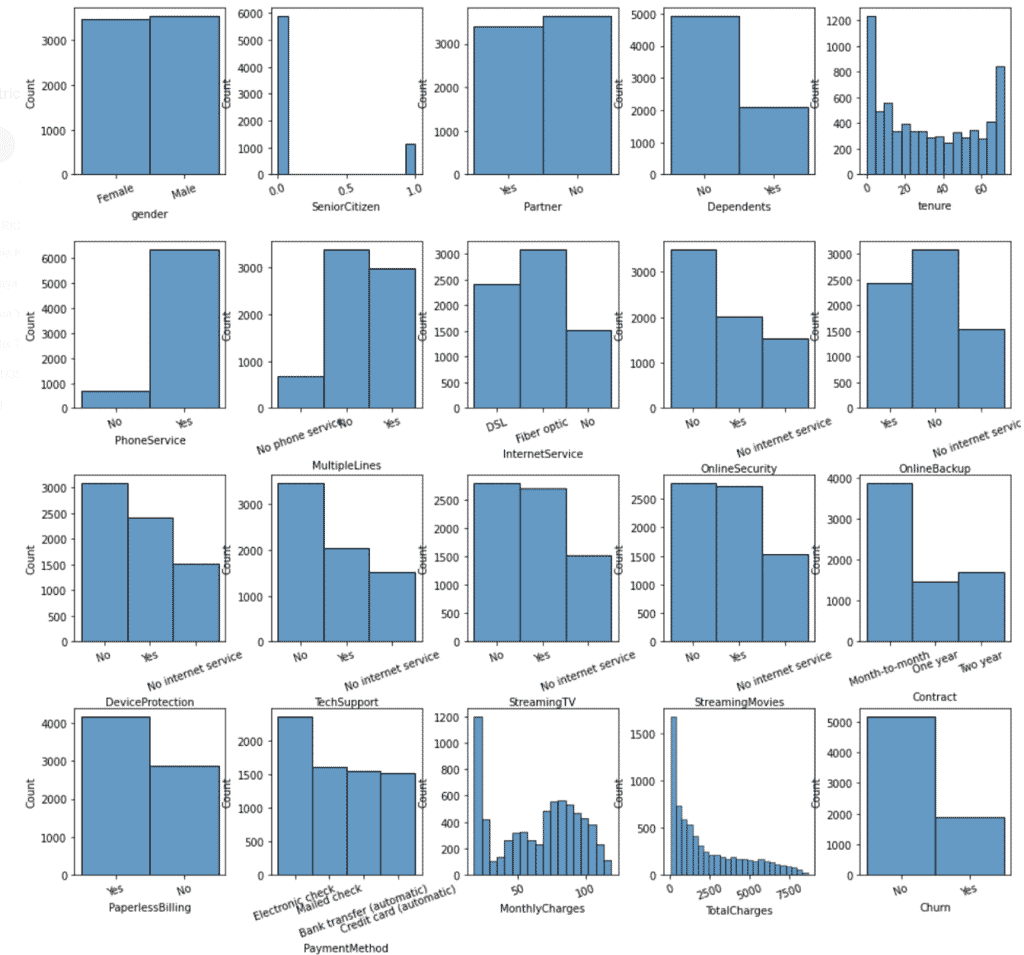
In der bivariaten Analyse betrachtet wir, wie zwei oder mehr Variablen einander beeinflussen. Das können entweder zwei numerische, zwei kategorische oder ein Mix aus beiden Variablen sein.
# Numerical-numerical variables
sns.pairplot(data = data_raw, hue='Churn')
plt.show()
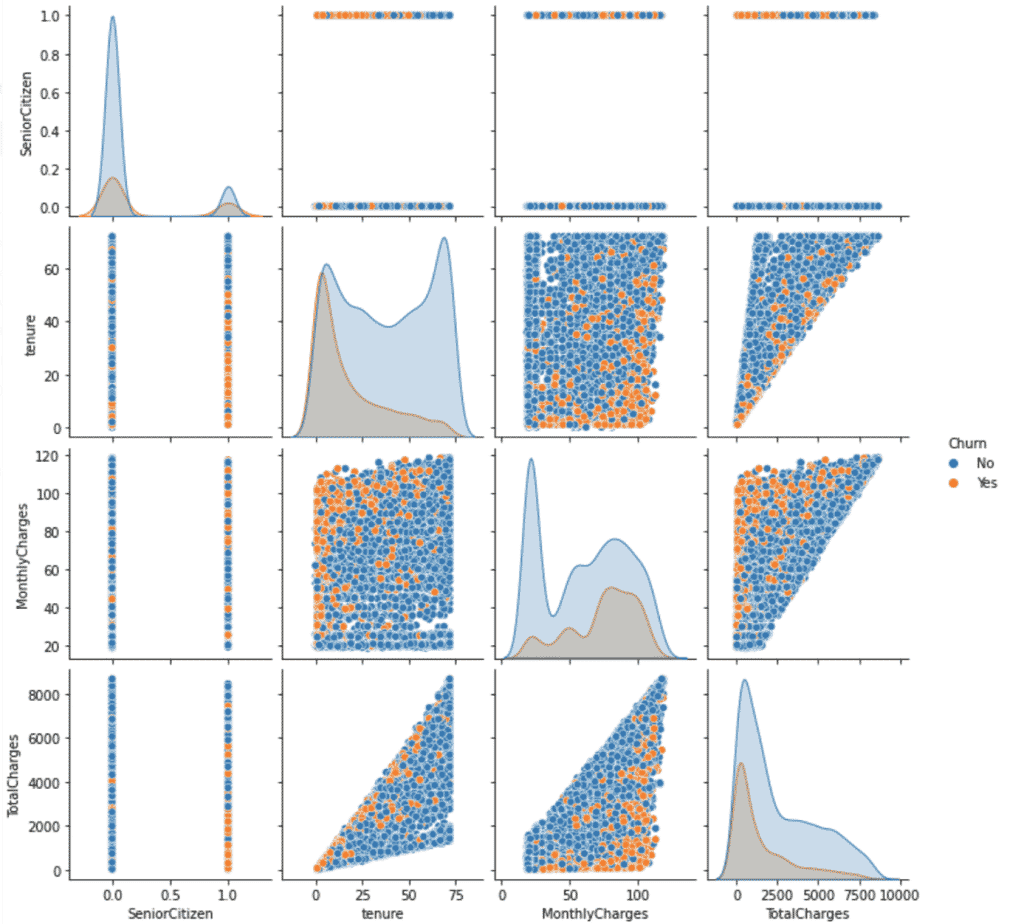
- Ergebnis:
Dass wir
hue='Churn'festgelegt haben, erlaubt es uns zwischen wechselnden und bestehenden Kunden zu unterscheiden. Man kann sehen, dass wechselnde Kunden zu einer kürzeren Anstellungszeit neigen, während sie gleichzeitig ein höheres Gehalt haben.
Lasst uns einen Blick auf die Beziehung zwischen kategorischen und numerischen Variablen werfen:
In diesem Fall erlaubt das uns Fragen wie „Neigen wechselnde Kunden dazu mehr zu verdienen?“, „Wann wechseln Kunden?“, oder „Neigen ältere Kunden eher dazu zu wechseln?“ zu beantworten.
Nutzt gerne den folgenden Code, um eigene Frage zu beantworten.
# Categorical-numerical variables
fig, axes = plt.subplots(nrows=1, ncols=3, figsize=(12, 6))
## Are churned customers likely to get charged more?
plt.subplot(1,3,1)
sns.boxplot(data_raw['Churn'], data_raw['MonthlyCharges'])
plt.title('MonthlyCharges vs Churn')
## When do customers churn?
plt.subplot(1,3,2)
sns.boxplot(data_raw['Churn'], data_raw['tenure'])
plt.title('Tenure vs Churn')
## Are senior citizen more likely to churn?
plt.subplot(1,3,3)
counts = (data_raw.groupby(['Churn'])['SeniorCitizen']
.value_counts(normalize=True)
.rename('percentage')
.mul(100)
.reset_index())
plot = sns.barplot(x="SeniorCitizen", y="percentage", hue="Churn", data=counts).set_title('SeniorCitizen vs Churn')
- Ergebnis:
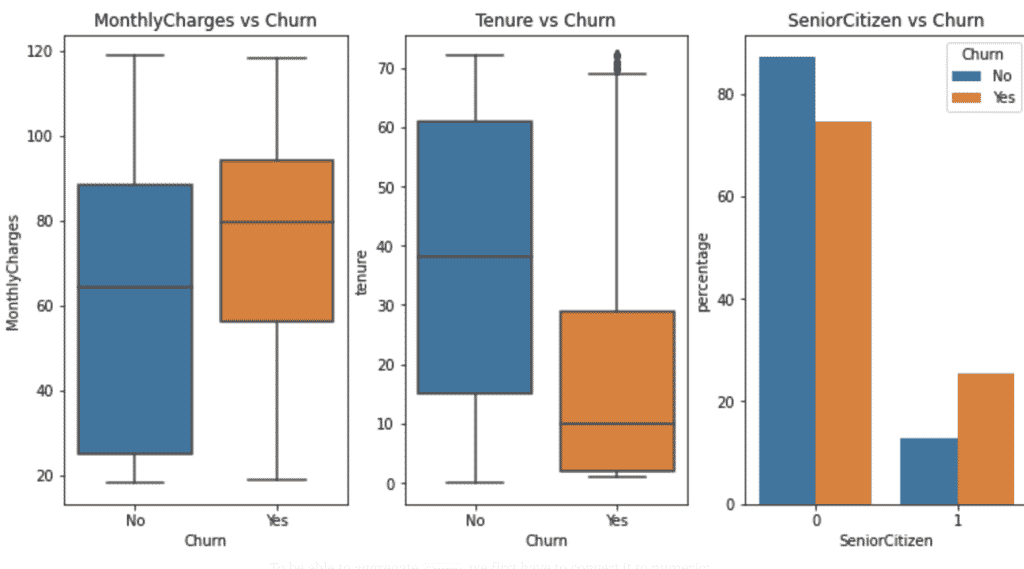
Kategorisch-kategorische Beziehungen helfen uns herauszufinden, wie der Wechsel sich, beispielsweise, anhand eines bestimmten Produktes oder verschiedener Zielgruppen unterscheidet. Wir erhalten Antworten zu Fragen wie „Wie sieht der Wechsel von verschiedenen Services aus?“, „Wechseln diejenigen, die technische Unterstützung erhalten, weniger oft? Oder „Neigt ein bestimmtes Geschlecht eher zu einem Wechsel?“
Nutzt den folgenden Code, um durch alle möglichen kategorisch-kategorischen Beziehungen Kombinationen durchzugehen.
for col in data_raw.select_dtypes(exclude=np.number):
sns.catplot(x=col, kind='count', hue='Churn',data=data_raw.select_dtypes(exclude=np.number))
Abschließend werfen wir einen kurzen Blick auf die multivariate Analyse– mit drei oder mehr Variablen. Eine gute Option, diese Beziehungen abzubilden, sind Heatmaps.
Um Churn verrechnen zu können, müssen wir die Variable zuerst zu numerisch konvertieren.
data_raw['Churn'] = data_raw['Churn'].map( {'No': 0, 'Yes': 1} ).astype(int)
Wir wählen ein Beispiel und erklären, wie man es interpretiert. Das ganze lässt sich aber auch auf alle anderen Kombinationen anwenden.
# How does PaymentMethod and Contract type affect churn?
## Create pivot table
result = pd.pivot_table(data=data_raw, index='PaymentMethod', columns='Contract',values='Churn')
## create heat map of education vs marital vs response_rate
sns.heatmap(result, annot=True, cmap = 'RdYlGn_r').set_title('How does PaymentMethod and Contract type affect churn?')
plt.show()
- Ergebnis:
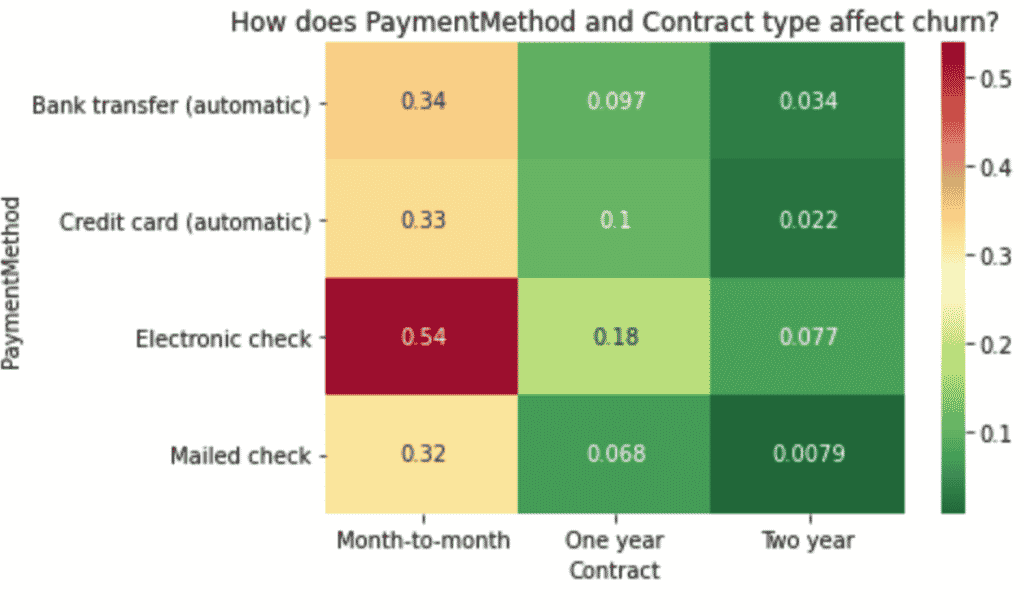
Schlussfolgerungen aus EDA
Da wir nun ein besseres Verständnis dafür haben, was in unseren Daten passiert, können wir bereits einige Schlussfolgerungen ziehen:
- Unsere Zielvariable ist nicht perfekt ausgeglichen. Das ist wichtig, wenn es um
die Wahl des Algorithmus geht und welche Bewertungsmetrik wir nutzen. - Die meisten Variablen im Datenset sind kategorisch
- Es gibt einige
NaNs, die wir unterstellen müssen. - Diejenigen, die mit elektronischen Checks bezahlen, wechseln am wahrscheinlichsten.
- Es sieht so aus, dass diejenigen, die einen monatlichen Vertrag haben, eher dazu neigen zu wechseln.
- Kunden, die technische Unterstützung erhalten, wechseln weniger
- Diejenigen, die Glasfaser im Vertrag haben, scheinen weniger zu wechseln im Vergleich zu denen, die DSL haben.
MonthlyChargesscheinen eine wichtige Rolle zu spielen, ob der Kunde beim Unternehmen bleibt oder nicht. Auf der einen Seite zahlen Kunden, die wechseln, im Schnitt fast 22% mehr. Auf der anderen Seite zahlen Senioren fast 34% mehr im Schnitt- und sogar 37%, wenn diese wechseln.SeniorCitizenneigen dazu, öfter zu wechseln und länger zu bleiben.- Die durchschnittliche
tenureist niedriger für wechselnde Kunden.
2. Vorverarbeitung- die Daten sortieren
Ziemlich sicher habt ihr schon gehört, dass Datenforscher über 80% ihrer Zeit damit verbringen Daten vorzubereiten. Dennoch gibt es einiges, was wir automatisieren können, und Tricks, mit denen wir uns selbst helfen können. Einer dieser Tricks ist eine Pipeline.
Eine Pipeline erstellen
Unsere besteht aus den vorverarbeiteten Schritten, gefolgt von einem Estimator am Ende der Pipeline. Das ist eine allgemeine Vorgehensweise, da die Pipelines von skikit learn´s bei allen Pipelineschritten fit_transform aufrufen. Bei der letzten wird lediglich fit aufgerufen. Abhängig von unseren Bedürfnissen können wir zum Beispiel, Imputation, Skalierung, Kodierung und Dimensionsreduktion einfügen.
Warum eine Pipeline für die Vorverarbeitung nutzen?
- Verhinderung von Datenlecks
Datenlecks passieren, wenn wir Informationen einfügen von Daten, die wir versucht haben, vorherzusagen während dem Training. Das passiert zum Beispiel, wenn wir die Bedeutung für die Zurechnung für das gesamte Datenset berechnen wollen, anstatt nur für die Trainingsdaten. Unsere Leistungseinschätzung wäre dann zu optimistisch. Eine Pipeline macht es einfach Datenlecks zu verhindern, da wir fit für die Trainingsdaten nutzen und predict für die Testdaten. - Fehlerreduzierung
Bei manuellen Vorverarbeitungen werden viele, kleinere Schritte benötigt und manchmal muss jede Variable einzeln durchgegangen werden. Eine Pipeline rationalisiert diesen Prozess und minimiert die Möglichkeit für Fehler.
- Besser aussehender Code
Die Pipeline wird einmal geschrieben und dann müssen wir lediglich die dazugehörige Methode benennen. Als Ergebnis erhalten wir einen Code, der einfacher zu lesen ist. - Kreuzvalidierung der gesamten Pipeline
Anstatt nur den Estimator kreuzvalidieren zu müssen, können wir die gesamte Pipeline kreuzvalidieren. Das Gleiche gilt für das Hyperparameter-Tuning.
Vorbereitende Schritte in unserer Pipeline
Zurechnung
Wir haben einige leere Ketten in TotalCharges entdeckt und zu NaN weitergereicht. Wir nutzen sci-kit learn’s SimpleImputer.- Skalierung
Algorithmen, die Distanzen zwischen Datenpunkten messen, funktionieren viel besser, wenn die Daten skaliert sind. Die Idee ist, verschiedene numerische Reichweite vergleichbar zu anderen zu machen. Wir nutzen scikit-learn’s StandardScaler. - Kategorisches Codieren
Wir haben gesehen, dass unser Datenset hauptsächlich kategorische Variablen enthält. Da die meisten machine-learning Systeme nicht-numerische Daten nicht verstehen, müssen wir diese in numerische konvertieren. Da alle Variablen eine sehr geringe Kardinalität haben, nutzen wir OneHotEncoder. - Variablen auswählen
Unsere Pipeline enthält einen Teil, in dem wir lediglich Variablen auswählen, die am besten funktionieren. Dafür nutzen wir scikit learn’s SelectKBest.
3. Trainingszeit- Modellaufbau und Vergleich
Datenteilung
Vor dem Start müssen wir sichergehen, dass wir die richtigen Daten in unser Modell eingeben. Wir teilen es in einen training und test Datensatz und teilen die Zielvariable vom Rest.
train, test = train_test_split(data_raw, test_size=0.25, random_state=123)
X = train.drop(columns='Churn', axis=1)
y = train['Churn']
Die Pipeline bauen
Stellt euch den preprocessor als eine Sammlung von Pipelines vor, wovon jede einzelne einen bestimmten Typ von Daten behandelt, eine für numerische und eine für kategorische Merkmale. ColumnTransformer lässt uns bestimmte Vorbereitungssschritte anwenden.
## Selecting categorical and numeric features
numerical_ix = X.select_dtypes(include=np.number).columns
categorical_ix = X.select_dtypes(exclude=np.number).columns
## Create preprocessing pipelines for each datatype
numerical_transformer = Pipeline(steps=[
('imputer', SimpleImputer(strategy='median')),
('scaler', StandardScaler())])
categorical_transformer = Pipeline(steps=[
('encoder', OrdinalEncoder()),
('scaler', StandardScaler())])
## Putting the preprocessing steps together
preprocessor = ColumnTransformer([
('numerical', numerical_transformer, numerical_ix),
('categorical', categorical_transformer, categorical_ix)],
remainder='passthrough')
Das beste Baseline-Modell finden
Die Idee ist den besten Algorithmus zu finden, der am besten auf als Basismodell funktioniert, das heißt ohne optimieren, und diesen auszuwählen, um ihn durch Hyperparameter-Tuning zu verbessern. Wir werden verschiedene Algorithmen durchlaufen, um zu sehen, welcher am besten funktioniert.
Wir nutzen roc_auc als Evaluationsmetrik.
## Creat list of classifiers we're going to try out
classifiers = [
KNeighborsClassifier(),
SVC(random_state=123),
DecisionTreeClassifier(random_state=123),
RandomForestClassifier(random_state=123),
AdaBoostClassifier(random_state=123),
GradientBoostingClassifier(random_state=123)
]
classifier_names = [
'KNeighborsClassifier()',
'SVC()',
'DecisionTreeClassifier()',
'RandomForestClassifier()',
'AdaBoostClassifier()',
'GradientBoostingClassifier()'
]
model_scores = []
## Looping through the classifiers
for classifier, name in zip(classifiers, classifier_names):
pipe = Pipeline(steps=[
('preprocessor', preprocessor),
('selector', SelectKBest(k=len(X.columns))),
('classifier', classifier)])
score = cross_val_score(pipe, X, y, cv=10, scoring='roc_auc').mean()
model_scores.append(score)
Nun ist es Zeit die Punkte zu vergleichen:
model_performance = pd.DataFrame({
'Classifier':
classifier_names,
'Cross-validated AUC':
model_scores
}).sort_values('Cross-validated AUC', ascending = False, ignore_index=True)
display(model_performance)
- Ergebnis:
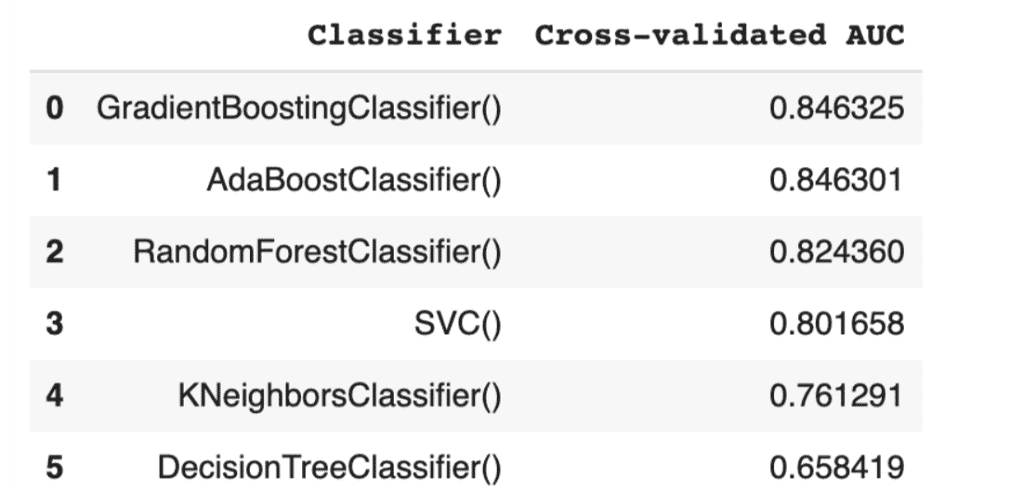
Hyperparameter Tuning
Nun, da wir unseren besten Kandidaten gefunden haben, können wir mit dem Hyperparameter-Tuning fortfahren. Das bedeutet grundsätzlich, die besten „Einstellungen“ für den Algorithmus zu finden.
Lasst uns unsere finale Pipeline bauen:
pipe = Pipeline(steps=[
('preprocessor', preprocessor),
('selector', SelectKBest(k=len(X.columns))),
('classifier', GradientBoostingClassifier(random_state=123))
])
Woher wissen wir was wir anpassen müssen?
Wir können jede Menge Hyperparameter innerhalb der gesamten Pipeline ändern. Werden wir alle versuchen? Nein! Kreuzvalidierung ist aufwendig und wir werden uns deshalb auf eine kleinere Anzahl an Hyperparametern konzentrieren. Wir können eine gesamte Liste von Hyperparametern mit pipe.get_params().keys() bekommen.
Die Idee hinter GridSearchCV ist, dass wir die Parameter spezifizieren und die zugehörigen Werte, die wir suchen wollen. GridSearch versucht alle möglichen Kombinationen und findet raus, welche am besten ist.
grid = {
"selector__k": k_range,
"classifier__max_depth":[1,3,5],
"classifier__learning_rate":[0.01,0.1,1],
"classifier__n_estimators":[100,200,300,400]
}
gridsearch = GridSearchCV(estimator=pipe, param_grid=grid, n_jobs= 1, scoring='roc_auc')
gridsearch.fit(X, y)
print(gridsearch.best_params_)
print(gridsearch.best_score_)
- Ergebnis:
{'classifier__learning_rate': 0.1, 'classifier__max_depth': 1, 'classifier__n_estimators': 400, 'selector__k': 16}
0.8501488378467128
4. Vorhersagen für neue Daten
Die test Daten helfen uns, eine genauere Einschätzung zur Performance von unserem Modell zu erhalten. Obwohl wir die Kreuzvalidierung durchgeführt haben, wollen wir das neue Modell auf neue Daten testen. Unsere Pipeline hat die Parameter aus den Trainingsdaten gelernt und wendet diese nun auf die Testdaten an.
## Separate features and target for the test data
X_test = test.drop(columns='Churn', axis=1)
y_test = test['Churn']
## Refitting the training data with the best parameters
gridsearch.refit
## Creating the predictions
y_pred = gridsearch.predict(X_test)
y_score = gridsearch.predict_proba(X_test)[:, 1]
## Looking at the performance
print('AUCROC:', roc_auc_score(y_test, y_score), '\nAccuracy:', accuracy_score(y_test, y_pred))
# Plotting the ROC curve
plot_roc_curve(gridsearch, X_test, y_test)
plt.show()
- Ergebnis:
AUCROC: 0.8441470897420832
Accuracy: 0.7927314026121521
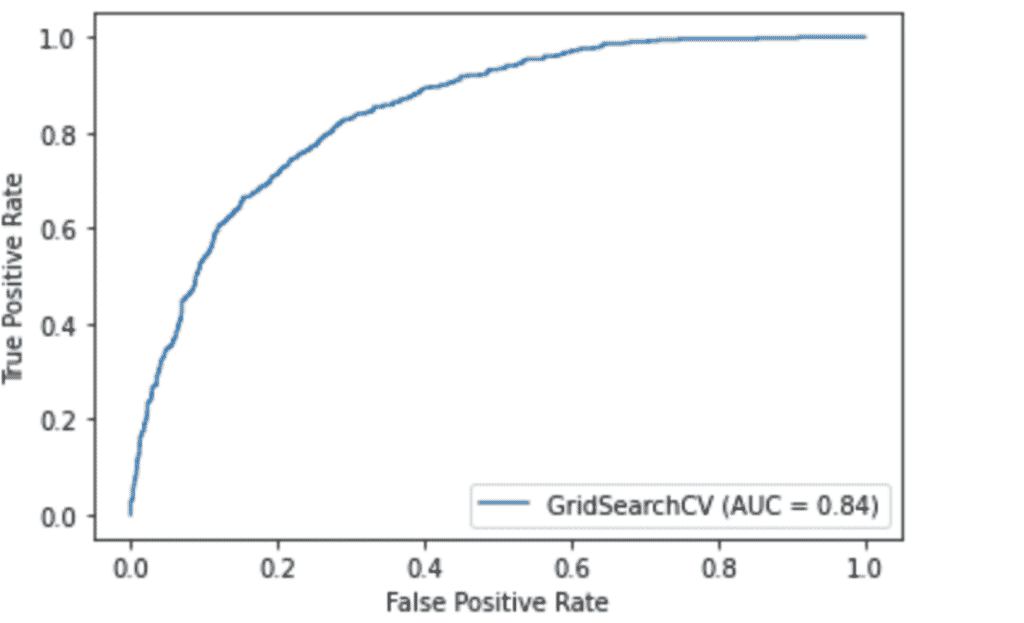
5. Schlussfolgerungen und abschließende Gedanken
In diesem Projekt haben wir mit Kundendaten gearbeitet, um ein Verständnis für Churn zu erlangen. Wir haben eine ausführliche Datenanalyse durchgeführt, um herauszufinden, welche Variablen sich auf den Wechsel auswirken. Wir haben gesehen, dass Kunden, die gewechselt sind, in der Regel mehr verdienen und oftmals einen monatlichen Vertrag haben.
Wir sind von rohen Daten, die einige falsch codierte Variablen hatten, einige fehlende Werte und jede Menge kategorische Daten, zu sauberen und richtigen Daten gekommen, durch die Automatisierung von unserer Vorverarbeitung mithilfe einer Pipeline.
Durch das Vergleichen verschiedener Klassifikatoren, haben wir das beste Baseline-Model ausgesucht und die Hyperparameter mit GridSearchCV angepasst.
Wir waren in der Lage Churn für neue Daten- das könnte in der Praxis beispielsweise für neue Kunden wichtig sein, mit einem AUC von 0,844 vorherzusagen.
Ein zusätzlicher Schritt, um die Performance unseres Modells zu erhöhen, wäre Feature-Engineering, also neue Merkmale schaffen, indem man bereits bestehende verändert oder kombiniert.
Ihr wollt an spannenden IT-Projekten arbeiten? Dann könnt ihr euch hier für die ElevateX-Community anmelden.








